Article
· Déc 16 12m de lecture

Présentation des fonctions de fenêtre SQL (2ème partie)

#Analytique #Outils #Performances #SQL #InterSystems IRIS

Dans la Partie 1, nous avons exploré le fonctionnement des fonctions de fenêtre. Nous avons découvert la logique sous-jacente à PARTITION BY, ORDER BY et à des fonctions telles que ROW_NUMBER() et RANK(). Dans cette deuxième partie, nous allons approfondir notre connaissance des fonctions de fenêtre au moyen d'exemples pratiques..

1. Fonctions d'agrégation sur fenêtre

Présentation

Ces fonctions calculent une agrégation (par exemple, somme, moyenne, minimum, maximum, nombre, etc.) sur la fenêtre définie, mais ne regroupent pas les lignes.
Chaque ligne reste visible, complétée par les valeurs agrégées pour sa partition.

Les fonctions prises en charge sont les suivantes:

  • AVG() — moyenne des valeurs dans la fenêtre.
  • SUM() — somme des valeurs dans la fenêtre.
  • MIN() — valeur minimale.
  • MAX() — valeur maximale.
  • COUNT() — nombre de lignes ou de valeurs non NULL.

Syntaxe:

function(...) OVER (PARTITION BY ... ORDER BY ...)

Exemple 1 — Analyse des salaires au niveau du département

Analysons comment le salaire de chaque employé se compare à la moyenne et à la rémunération totale de son département.

CREATE TABLE Employees (
    Department VARCHAR(50),  
    EmployeeName VARCHAR(50),  
    Salary INTEGER  
)

INSERT INTO Employees  
SELECT 'HR','Anna',5200 UNION ALL
SELECT 'HR','John',6000 UNION ALL
SELECT 'HR','Maria',5500 UNION ALL
SELECT 'IT','Paul',7200 UNION ALL
SELECT 'IT','Laura',6800 UNION ALL
SELECT 'Finance','Alice',8000 UNION ALL
SELECT 'Finance','Robert',7900

Nous devons procéder comme suit :

  • Calculer le salaire moyen pour chaque département à l'aide de AVG() OVER (PARTITION BY Department).

  • Calculer la différence entre le salaire de chaque employé et la moyenne pour son département (DiffFromAvg).

  • Déterminer les dépenses salariales totales pour chaque département à l'aide de SUM() OVER (PARTITION BY Department).

  • Afficher toutes les lignes des employés avec ces mesures calculées.
  • Trier le résultat final par Département, puis par Salaire (le plus élevé en premier).
SELECT  
    Department,  
    EmployeeName,  
    Salary,  
    AVG(Salary) OVER (PARTITION BY Department) AS AvgDeptSalary,
    Salary - AVG(Salary) OVER (PARTITION BY Department) AS DiffFromAvg,
    SUM(Salary) OVER (PARTITION BY Department) AS DeptTotal  
FROM Employees  
ORDER BY Department, Salary DESC

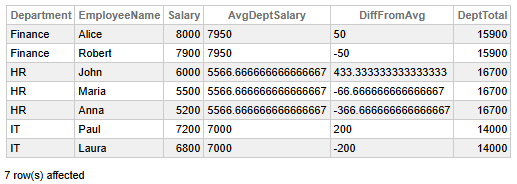image
Fig 1 - Analyse des salaires au niveau du département

Les données ci-dessus nous permettent de tirer les conclusions suivantes :

  • Les salaires au niveau du département financier sont proches de la moyenne : Alice gagne un peu plus (+50), Robert un peu moins (−50), ce qui indique une rémunération équilibrée.
  • Le département des ressources humaines révèle une disparité salariale importante : John gagne bien plus que la moyenne (+433,33), tandis qu'Anna gagne bien moins (−366,67), ce qui suggère une potentielle inégalité ou une différenciation basée sur les rôles.
  • Le salaire de Maria dans les ressources humaines est proche de la moyenne (−66,67), se situant à mi-chemin entre les extrêmes.
  • Le service informatique présente un écart symétrique : Paul gagne 200 de plus que la moyenne, Laura 200 de moins, ce qui implique une nette différenciation salariale.
  • Les totaux par service montrent que les ressources humaines ont le salaire global le plus élevé (16 700), suivies par les finances (15 900) et l'informatique (14 000), ce qui reflète peut-être les effectifs ou la répartition du budget.
  • Salaire moyen par service : Finance (7 950), RH (5 566,67), Informatique (7 000), les RH étant nettement inférieures, ce qui souligne les différents niveaux d'emploi ou les taux du marché.

👉 Pourquoi est-ce utile ? Vous pouvez comparer les individus à leur groupe (moyenne du service) sans réduire l'ensemble de données. C'est idéal pour identifier les valeurs aberrantes ou les déséquilibres salariaux.

Exemple 2 — Analyse de la charge de travail de la clinique

Évaluons la charge de travail quotidienne de chaque médecin par rapport au total de son service.

CREATE TABLE Appointments (  
    Department VARCHAR(50),  
    Physician VARCHAR(50),  
    DailyAppointments INTEGER  
)

INSERT INTO Appointments  
SELECT 'Cardiology','Dr. Smith',18 UNION ALL
SELECT 'Cardiology','Dr. Lee',22 UNION ALL
SELECT 'Cardiology','Dr. Adams',16 UNION ALL
SELECT 'Pediatrics','Dr. Young',25 UNION ALL
SELECT 'Pediatrics','Dr. Patel',30 UNION ALL
SELECT 'Neurology','Dr. Miller',15

Nous devons procéder comme suit :

  • Calculer le nombre total de rendez-vous quotidiens pour chaque département à l'aide d'une fonction de fenêtre (SUM() OVER (PARTITION BY Department)).
  • Déterminer le pourcentage du total des rendez-vous du service fourni par chaque médecin (WorkloadPercentage).
  • Afficher toutes les lignes individuelles médecin/rendez-vous à côté de ces totaux et pourcentages calculés pour le service.
  • Trier le résultat final par Service, puis par Rendez-vous quotidiens (du plus élevé au plus bas).
SELECT  
    Department,  
    Physician,  
    DailyAppointments,  
    SUM(DailyAppointments) OVER (PARTITION BY Department) AS DeptTotalAppointments,  
    ROUND(  
        100.0 * DailyAppointments /
        SUM(DailyAppointments) OVER (PARTITION BY Department), 2  
    ) AS WorkloadPercentage  
FROM Appointments  
ORDER BY Department, DailyAppointments DESC

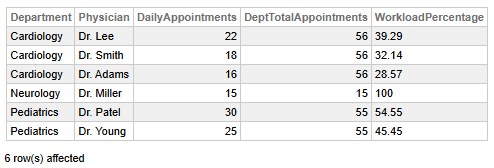image
Fig 2 - Analyse de la charge de travail de la clinique

  • Le service de cardiologie présente une répartition équilibrée de la charge de travail : Dr Lee traite la plus grande partie (39,29 %), suivi par Dr Smith (32,14 %) et Dr Adams (28,57 %), ce qui indique qu'il n'y a pas de disparités extrêmes.
  • Le service de neurologie est composé d'un seul médecin : Dr Miller assume 100 % de la charge de travail, ce qui suggère une responsabilité totale et une dépendance potentielle excessive à l'égard d'un seul prestataire.
  • Le service de pédiatrie présente un déséquilibre modéré : Dr Patel gère une part plus importante (54,55 %) que Dr Young (45,45 %), ce qui indique une charge de travail légèrement inégale.
  • Nombre total de rendez-vous par service : cardiologie (56), pédiatrie (55), neurologie (15), la cardiologie et la pédiatrie ayant des volumes similaires, tandis que la neurologie affiche un volume nettement inférieur.
  • Charge de travail individuelle la plus élevée : Dr Patel (30 rendez-vous), suivi du Dr Lee (22), ce qui implique des considérations potentielles en matière de planification ou de capacité.

👉 Pourquoi cela est utile : comprendre la contribution de chaque médecin à la charge de travail du service est idéal pour équilibrer les ressources.

2. Fonctions de classement et de distribution

Présentation

Ces fonctions attribuent des classements ou des distributions aux lignes d'une partition.
Contrairement aux agrégats, elles fournissent une position relative ou un contexte centile.

Fonctions :

  • ROW_NUMBER() — un entier séquentiel unique attribué à chaque ligne.
  • RANK() — attribue des classements avec des écarts en cas d'égalité.
  • DENSE_RANK() — détermine les classements sans écarts.
  • NTILE(num_groups) — divise les lignes en groupes à peu près égaux et renvoie le numéro du groupe.
  • PERCENT_RANK() — un classement fractionnaire, calculé comme (classement-1)/(lignes-1).
  • CUME_DIST() — distribution cumulative, calculée comme les lignes avec une valeur ≤ valeur de la ligne actuelle / nombre total de lignes.

Exemple 1 — Classement de satisfaction des services hospitaliers

Évaluons le score de satisfaction moyen de chaque service hospitalier au sein de l'organisation.

CREATE TABLE DepartmentSatisfaction (  
    Department VARCHAR(50),  
    Month VARCHAR(10),
    AvgSatisfaction DECIMAL(5,2)  
)

INSERT INTO DepartmentSatisfaction  
SELECT 'Cardiology','Jan',4.6 UNION ALL
SELECT 'Cardiology','Feb',4.8 UNION ALL
SELECT 'Cardiology','Mar',4.9 UNION ALL
SELECT 'Neurology','Jan',4.7 UNION ALL
SELECT 'Neurology','Feb',4.7 UNION ALL
SELECT 'Neurology','Mar',4.9 UNION ALL
SELECT 'Pediatrics','Jan',4.9 UNION ALL
SELECT 'Pediatrics','Feb',4.8 UNION ALL
SELECT 'Pediatrics','Mar',4.9 UNION ALL
SELECT 'Oncology','Jan',4.5 UNION ALL
SELECT 'Oncology','Feb',4.7 UNION ALL
SELECT 'Oncology','Mar',4.7

Nous devons procéder comme suit :

  • Calculer le score de satisfaction moyen pour chaque département à l'aide de AVG() OVER dans une requête groupée.
  • Appliquer trois fonctions de classement pour comparer les comportements :
    • ROW_NUMBER() pour un classement strict.
    • RANK() pour afficher les écarts dans le classement en cas d'égalité.
    • DENSE_RANK() pour regrouper les départements à égalité sans écart.
  • Trier le résultat final par satisfaction moyenne (la plus élevée en premier)..
SELECT  
    Department,  
    ROUND(AVG(AvgSatisfaction),2) AS DeptAvgSatisfaction,
    ROW_NUMBER() OVER (ORDER BY AVG(AvgSatisfaction) DESC) AS AvgSatisfactionRowNumber,
    RANK() OVER (ORDER BY AVG(AvgSatisfaction) DESC) AS AvgSatisfactionRankValue,
    DENSE_RANK() OVER (ORDER BY AVG(AvgSatisfaction) DESC) AS AvgSatisfactionDenseRankValue
FROM DepartmentSatisfaction  
GROUP BY Department
ORDER BY DeptAvgSatisfaction DESC

image
Fig 3 - Classement de satisfaction des services hospitaliers

Ces données nous permettent de tirer les conclusions suivantes:

  • La pédiatrie arrive en tête en termes de satisfaction avec le score moyen le plus élevé (4,87), obtenant ainsi la première place dans tous les indicateurs.
  • La cardiologie et la neurologie obtiennent le même score moyene de satisfaction (4,77), ce qui les place ex æquo à la deuxième place dans les systèmes de classement standard et dense.
  • L'oncologie obtient le score de satisfaction le plus bas (4,63), ce qui la place en dernière position dans le classement par rang et par valeur, mais en troisième position dans le classement dense en raison de l'égalité mentionnée ci-dessus.
  • Les scores de satisfaction sont très proches les uns des autres, avec un écart de seulement 0,24 entre le plus élevé et le plus bas, ce qui indique un niveau de satisfaction généralement élevé dans tous les services.

👉 Pourquoi est-ce utile ? La comparaison des performances des services à l'aide de vues de classement flexibles (ROW_NUMBER() pour un ordre unique, RANK() pour les écarts concurrentiels et DENSE_RANK() pour les ex aequo groupés) est idéale pour les tableaux de bord de performance ou les classements.

Exemple 2 — Classement des performances des produits

Évaluons les performances commerciales de chaque produit par rapport à celles des autres produits de sa catégorie à l'aide de fonctions de classement basées sur des percentiles.

CREATE TABLE Sales (  
    Category VARCHAR(50),  
    Product VARCHAR(50),  
    Sales INTEGER  
)

INSERT INTO Sales  
SELECT 'Electronics','Phone',1200 UNION ALL
SELECT 'Electronics','Tablet',900 UNION ALL
SELECT 'Electronics','TV',1500 UNION ALL
SELECT 'Electronics','Camera',1100 UNION ALL
SELECT 'Furniture','Chair',400 UNION ALL
SELECT 'Furniture','Table',700 UNION ALL
SELECT 'Furniture','Desk',650

Nous devons :

  • Diviser les produits en quartiles au sein de chaque catégorie à l'aide de NTILE(4) OVER (PARTITION BY Category ORDER BY Sales DESC).
  • Calculer le rang centile de chaque produit à l'aide de PERCENT_RANK() OVER (PARTITION BY Category ORDER BY Sales).
  • Calculer la distribution cumulative à l'aide de CUME_DIST() OVER (PARTITION BY Category ORDER BY Sales).
  • Trier le résultat final par Catégorie, puis par Ventes (les plus élevées en premier).
SELECT  
    Category,  
    Product,  
    Sales,  
    NTILE(4) OVER (PARTITION BY Category ORDER BY Sales DESC) AS Quartile,  
    PERCENT_RANK() OVER (PARTITION BY Category ORDER BY Sales) AS PercentRank,
    CUME_DIST() OVER (PARTITION BY Category ORDER BY Sales) AS CumulativeDist
FROM Sales  
ORDER BY Category, Sales DESC

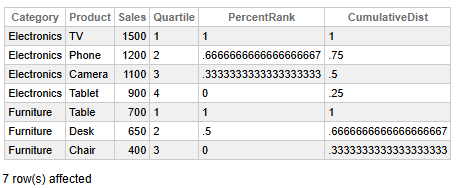image
Fig 4 - Classement des performances des produits

Ces données nous permettent de tirer les conclusions suivantes :

  • Les téléviseurs et les tables sont les produits les plus vendus dans leurs catégories respectives, tous deux classés dans le quartile 1 avec des scores PercentRank et CumulativeDist parfaits de 1.
  • Les appareils électroniques affichent une tendance à la baisse des ventes par rapport aux téléviseurs et aux tables, chaque produit occupant un quartile et un rang centile inférieurs, ce qui indique une distribution des performances bien stratifiée.
  • Les ventes de meubles diminuent également de la table à la chaise. Cependant, la baisse est plus forte et moins uniformément répartie, ce qui suggère une demande plus concentrée pour les articles haut de gamme.
  • Table et Chaise sont les moins performants dans leurs catégories respectives, avec un PercentRank de 0 et un CumulativeDist inférieur à 0,35, ce qui indique un impact relatif minimal sur les ventes.
  • Les téléphones et les bureaux occupent des positions intermédiaires dans leurs catégories, avec des PercentRanks compris entre 0,5 et 0,67, ce qui reflète des performances modérées.

👉 Pourquoi est-ce utile? Identifier les produits les plus performants et les classer par centile pour les tableaux de bord est idéal pour la stratégie commerciale et la planification des stocks.

Exemple 3 — Quartiles de performance des hôpitaux

Classons les services hospitaliers en fonction de leur volume mensuel de patients à l'aide de quartiles et d'une distribution cumulative.

CREATE TABLE DepartmentMetrics (  
    Department VARCHAR(50),  
    PatientCount INTEGER  
)

INSERT INTO DepartmentMetrics  
SELECT 'Cardiology',1200 UNION ALL
SELECT 'Pediatrics',950 UNION ALL
SELECT 'Neurology',800 UNION ALL
SELECT 'Orthopedics',700 UNION ALL
SELECT 'Dermatology',500 UNION ALL
SELECT 'Oncology',600

Nous devons procéder comme suit :

  • Utiliser NTILE(4) pour diviser les services en quartiles en fonction du nombre de patients (PatientCount).
  • Appliquer CUME_DIST() pour calculer la distribution cumulative des services en fonction du volume de patients.
  • Trier le résultat final par PatientCount (ordre croissant) pour visualiser les niveaux de performance.
SELECT  
    Department,  
    PatientCount,  
    NTILE(4) OVER (ORDER BY PatientCount) AS Quartile,  
    CUME_DIST() OVER (ORDER BY PatientCount) AS CumulativeDistribution
FROM DepartmentMetrics  
ORDER BY PatientCount

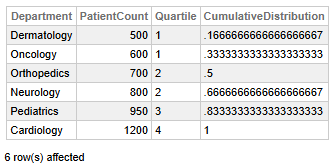image
Fig 5 - Quartiles de performance des hôpitaux

Ces données nous permettent de dégager les conclusions clés suivantes:

  • La cardiologie compte le plus grand nombre de patients (1 200), ce qui la place dans le quartile 4 avec une distribution cumulative complète (1), indiquant que ce département dessert la plus grande part de patients.
  • La dermatologie et l'oncologie se situent dans le quartile 1 avec un nombre de patients plus faible (500 et 600), représentant le tiers inférieur des volumes des services.
  • L'orthopédie et la neurologie se situent dans la moyenne, au quartile 2, avec respectivement 700 et 800 patients, ce qui correspond à des niveaux de service modérés.
  • La pédiatrie se classe au quartile 3 avec 950 patients, ce qui suggère un volume supérieur à la moyenne, mais pas le plus élevé.

👉 Pourquoi est-ce utile ? Classer rapidement les services en fonction de leur performance facilite la gestion hospitalière et est idéal pour l'allocation des ressources et la planification stratégique.

3. Conclusion

Restez connectés pour lire la dernière partie de cette introduction aux fonctions de fenêtre, où nous explorerons un autre groupe de fonctions très puissantes. Vous obtiendrez également des conseils d'optimisation des performances et un guide pratique pour vous aider à décider quand utiliser les fonctions de fenêtre et quand les éviter.

Cet article a été rédigé avec l’aide d’outils d’intelligence artificielle afin de clarifier les concepts et d’en améliorer la lisibilité.

Consultez l'article de la documentation InterSystems lié
Discussion (0)2
Connectez-vous ou inscrivez-vous pour continuer